Système décimal et binaire

Le système décimal, couramment intégré dans les mathématiques quotidiennes, se distingue nettement du système binaire, principalement utilisé dans le secteur de l'informatique. Le système décimal, basé sur dix chiffres (de 0 à 9), est la pierre angulaire de la plupart des calculs effectués dans notre vie de tous les jours, facilitant les opérations telles que l'addition, la soustraction, la multiplication, et la division. Il reflète la manière dont les êtres humains ont historiquement compté et mesuré les objets autour d'eux, probablement en raison du nombre total de doigts sur les mains.

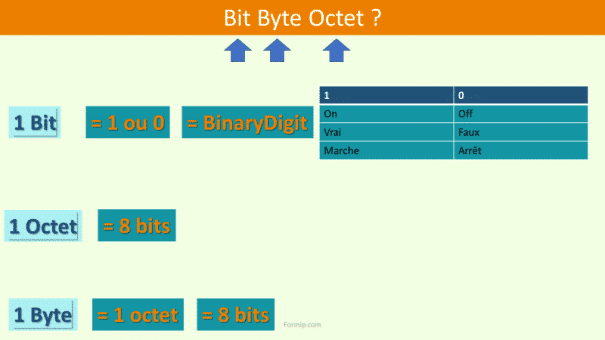
À l'opposé, le système binaire, constitué uniquement de deux chiffres (0 et 1), est la fondation sur laquelle repose la technologie informatique moderne. Ce système simplifié permet de représenter de façon efficace les états on (1) et off (0) des circuits électroniques. Grâce à sa simplicité, il s'adapte parfaitement à la logique des ordinateurs et des appareils numériques, qui utilisent des milliards de transistors pour traiter et stocker des informations.

Concernant les périphériques réseau, ils dépendent exclusivement du système binaire pour identifier leur position sur le réseau. Que ce soit pour attribuer des adresses IP, calculer des sous-réseaux, ou gérer des données en transit, le binaire offre une précision et une clarté indispensables dans l'architecture réseau. Cette dépendance souligne l'importance cruciale de comprendre le fonctionnement du binaire dans le domaine des technologies de l'information et de la communication (TIC), où la rapidité et l'efficacité de la transmission des données sont primordiales.

En somme, la distinction entre ces deux systèmes numériques illustre l'évolution des outils mathématiques, passant de méthodes adaptées aux activités humaines générales à des applications spécialisées répondant aux exigences spécifiques de la technologie moderne. Comprendre ces différences est essentiel pour les professionnels de l'informatique, les ingénieurs réseau, et toute personne s'intéressant à la manière dont nos dispositifs calculent, communiquent et interagissent dans un monde de plus en plus numérisé.

Pour une meilleure compréhension du fonctionnement des réseaux, il est essentiel d'avoir une connaissance solide des bases du système binaire.

Dans le système décimal, que nous utilisons fréquemment, les chiffres varient de 0 à 9, puis passent à 10 jusqu'à 99, avant de recommencer avec le chiffre "100" et d'augmenter de "+ 1" à chaque itération.

En revanche, dans le système binaire, seuls les chiffres 0 et 1 sont utilisés. Le premier chiffre est 0, suivi de 1, puis du chiffre 10, 11, 100, 101, et ainsi de suite...

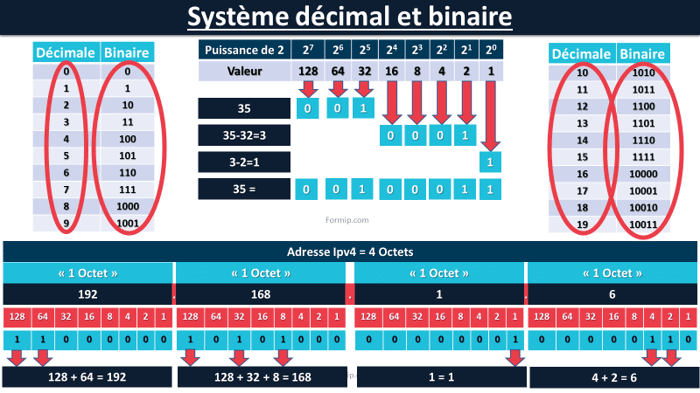
Ici, vous voyez la conversion binaire des chiffres décimaux de 0 à 19 !

Pour convertir les nombres décimaux en binaires, il est crucial d'adopter un processus spécifique, basé sur les puissances de 2. Cette méthode implique de décomposer le nombre décimal en une somme de puissances de 2, permettant ainsi de traduire chaque valeur décimale en son équivalent binaire. C'est une étape fondamentale pour comprendre et travailler efficacement avec les systèmes numériques en informatique.

Dans la 1ʳᵉ ligne du tableau, vous avez les puissances de 2. Et juste en dessous la valeur décimale de ces puissances !

Pour illustrer, convertissons le chiffre 35 en binaire. Ce processus démontre comment traduire des valeurs décimales en séquences binaires, une compétence clé en informatique.

En regardant le tableau, de gauche à droite, il faut se demander quelle est la plus grande puissance de 2 qui est inférieure ou égale à 35.

128 est supérieur à 35, alors on met un 0.

64 est également supérieur à 35, ce sera donc aussi un zéro en dessous.

Par contre, 32 est inférieur à 35. Comme il est inférieur ou égal à 35, on lui met un « 1 » en dessous.

Ensuite il faut calculer la quantité qui reste en soustrayant 32 de 35. Il nous reste donc 3.

On continue la même logique, toujours de gauche à droite, mais cette fois-ci avec le chiffre 3.

16 est supérieur au chiffre « 3 », on lui mettra donc un 0

8 est toujours supérieur à 3, ce sera donc un 0

Idem pour 4, on lui met aussi un 0.

Quant au chiffre d’à côté, le 2. Il est bien inférieur ou égal à 3, cette fois-ci, on met un « 1 ».

On soustrait 2 du chiffre 3, et il nous reste plus qu’à trouver le chiffre « 1 » !

La valeur décimale du dernier bit est 1, ce qui correspond au nombre restant. On mettra donc un 1 en dessous.

L'équivalent binaire du nombre décimal 35 est 00100011.

Une adresse IP se présente sous la forme de quatre ensembles de nombres décimaux séparés par des points.

Le nombre décimal dans chaque ensemble est compris entre 0 et 255. Chaque parti fait 1 octet.

Il y a donc quatre octets dans une adresse IP.

Tous les systèmes informatiques comprennent les adresses IP uniquement sous forme binaire.

On va maintenant traduire cette adresse IP en binaire !

Le plus simple pour traduire d’une forme décimale en binaire est de commencer par écrire les puissances de 2, pour chaque parti de notre adresse IP !

Il nous suffit maintenant d'appliquer la même méthode que celle utilisée pour le 35 ! Un processus éprouvé qui assure succès et efficacité, nous menant vers notre objectif !

• La valeur du premier ensemble est 192. Il s’agit de l’addition de 128 et 64 !
• Ensuite, nous avons 168, qui est l’addition de 128 + 32 + 8 !
• Le 1 correspond uniquement à la puissance la plus à droite !
• Et le 6 est la somme de 4 + 2 !

N’hésitez pas à vous entraîner chez vous à la conversion binaire et vérifier le résultat sur Google à l’aide de n’importe quel convertisseur que vous pouvez trouver. Il est primordial de savoir convertir soi-même sur papier n’importe quelle adresse IP. Surtout pour le CCNA !

Découvrez sur la chaîne YouTube de Formip une gamme complète de cours dédiés à la réussite du CCNA. Optimisez vos compétences en réseaux avec des modules pédagogiques ciblés, conçus pour guider étudiants et professionnels à travers tous les aspects essentiels de la certification Cisco CCNA.